A square is inscribed in a circle. Find the ratio of the areas of the circle and the square.
Given:
A square is inscribed in a circle.
Let the radius of circle be ‘r’ and the side of the square be ‘x’.
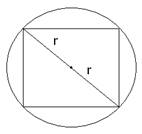
⇒ The length of the diagonal = 2r
∵ Length of side of square = ![]()
∴ Length of side of square = ![]() = √2r
= √2r
Area of square = side × side = x × x = √2r × √2r = 2r2
Area of circle = πr2
Ratio of areas of circle and square = ![]() =
= ![]() =
= ![]()
Hence, the ratio of areas of circle and square is π:2.
17