In the given figure, O is the centre of the bigger circle, and AC is its diameter. Another circle with AB as diameter is drawn. If AC = 54 cm and BC = 10 cm, find the area of the shaded region.

Question

Philoid · Accepted Answer

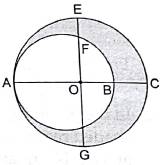
Given:

AC = 54 cm

BC = 10 cm

⇒ AB = AC-BC = 54-10 = 44 cm

Radius of bigger circle = = = 27 cm = r₁

Radius of Smaller circle = = = 22 cm = r₂

∵ Area of Circle = πr²

∴ Area of Bigger Circle = πr₁²

= × 27 × 27

= cm²

Similarly, Area of Smaller Circle = πr₂²

= × 22 × 22

= cm²

Area of shaded region = Area of Bigger Circle – Area of Smaller Circle = - = = 770 cm²

Hence, Area of Shaded Region is 770 cm².