From a thin metallic piece in the shape of a trapezium ABCD in which AB ∥ CD and ∠BCD = 90°, a quarter circle BFEC is removed. Given, AB = BC = 3.5 cm and DE = 2 cm, calculate the area of remaining (shaded) part of metal sheet.
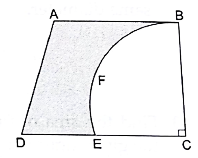
Given:
AB ∥ CD
∠BCD = 90°
AB = BC = 3.5 cm = EC
DE = 2 cm
DC = DE + EC = 2 + 3.5 = 5.5 cm
Area of Trapezium = 
× Sum of Parallel Sides × h
= 
× (AB + DC) × BC
= 
× (3.5 + 5.5) × 3.5
= 
× 9 × 3.5
= 15.75 cm2
Area of Quadrant BFEC = 
× πr2 = 
× 
× 3.5 × 3.5
= 9.625 cm2
Thus, Area of remaining part of metal sheet
= Area of Trapezium – Area of Quadrant BFEC
= 15.75 – 9.625 = 6.125 cm2
Hence, the area of the remaining part of metal sheet is 6.125 cm2.
50