Given, the circumference of a circle exceeds its diameter by 45 cm.

⇒ Circumference of circle = Diameter of circle + 45

Let ‘d’ = diameter of the circle

⇒ Circumference = d + 45 → eqn1

And we know, Circumference of a circle = 2πr → eqn2

Where r = radius of circle

Also, we know that the radius of the circle is half of its diameter.

Put value of circumference in equation 1 from equation 2

⇒ 2πr = d + 45 → eqn4

Put value of r in equation 4 from equation 3

⇒ πd = d + 45

⇒ πd – d = 45

⇒ (π – 1)d = 45 (taking d common from L.H.S)

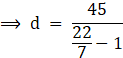
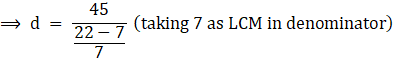
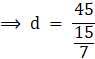
On rearranging, we get

⇒ d = 21 cm

Therefore, the diameter of the circle is 21 cm.

Thus, the radius of the circle

⇒ r = 10.5 cm

Now put the value of r in equation 2, we get

= 66 cm

The circumference of the circle is 66 cm.