Book: RS Aggarwal - Mathematics
Chapter: 18. Area of Circle, Sector and Segment
Subject: Maths - Class 10th
Q. No. 4 of Exercise 18B
Listen NCERT Audio Books - Kitabein Ab Bolengi
A copper wire when bent in the form of a square encloses an area of 484 cm2. The same wire is now bent in the form of a circle. Find the area enclosed by the circle.
In this question the wire is first bent in the shape of square and then same wire is bent to form a circle. The point to be noticed is that the same wire is used both the times which implies that the perimeter of square and that of circle will be equal.
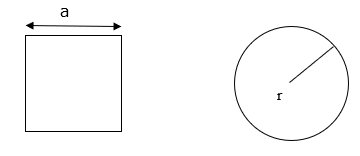
Let the square be of side ‘a’ cm and radius of the circle be ‘r’
Given the area enclosed by the square = 484 cm2
Also, we know that Area of square = Side × Side
Area of the square = a2
⇒ a2 = 484
⟹ a = √484
⇒ a = 22 cm
Therefore, side of square, ‘a’ is 22 cm.
Also, circumference of the circle = Perimeter of square → eqn1
Perimeter of square = 4 × side
Perimeter of square = 4×22
⇒ Perimeter of square = 88 cm → eqn2
Also, we know, Circumference of circle = 2πr → eqn3
Put values in equation 1 from equation 2 & 3, we get
2πr = 88
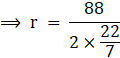
On rearranging,
⇒ r = 14 cm
So, the radius ‘r’ of the circle is 14 cm.
Area of circle = πr2
Where r = radius of the circle
= π(142)
= 4312/7
= 616 cm2
Area of the circle is 616 cm2.
