The sum of the radii of two circles is 7 cm, and the difference of their circumferences is 8 cm. Find the circumferences of the circles.
Given Sum of the radius of the circles = 7 cm
the difference of their circumference = 8 cm
Let the radius one circle be ‘r1’ cm and other be ‘r2’ cm and circumference be ‘C1’ and ‘C2’ respectively.
Also, circumference of circle = 2πr
Where r = radius of the circle
C1 = 2πr1 and C2 = 2πr2
r1 + r2 = 7 → eqn1
C1 – C2 = 8 → eqn2
(Note: Her it is considered that r1>r2)
We can rewrite equation 2 as,
2πr1 – 2πr2 = 8
⇒ 2π(r1 – r2) = 8
(taking 2π common from L.H.S)
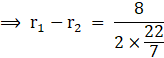
Put the value of r1 from equation 3 in equation 1
(taking 11 as LCM on R.H.S)
Put value of r2 in equation 3
(from equation 3)
(taking 22 as LCM on R.H.S)
(by putting value of r1)
= 182/7
= 26 cm
(by putting value of r2)
= 126/7
= 18 cm
The circumference of circles are 26 cm and 18 cm.