Book: RS Aggarwal - Mathematics
Chapter: 18. Area of Circle, Sector and Segment
Subject: Maths - Class 10th
Q. No. 10 of Exercise 18B
Listen NCERT Audio Books to boost your productivity and retention power by 2X.
A racetrack is in the form of a ring whose inner circumference is 352 m and outer circumference is 396 m. Find the width and the area of the track.
Consider the race track as shown below,
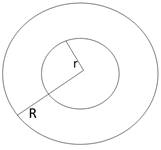
The inner and outer radius of track is ‘r’ cm and ‘R’ cm respectively.
Let inner and outer circumference be ‘C1’ and C2’ respectively.
C1 = 352 m and C2 = 396 m.
We know,
Circumference of circle = 2πr
Where r = radius of the circle
C1 = 2πr and C2 = 2πR
⇒ 2πr = 352 and 2πR = 396
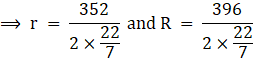
On rearranging,
⇒ r = 56 m and R = 63 m
So, the width of the race track = R – r,
⇒ Width of the race track = 63 – 56
⇒ Width of the race track = 7 m
Area of race track = area of outer circle – area of inner circle
⇒ Area of track = πR2 – πr2 (put values of r and R)
⇒ Area of track = π(632) – π(562)
⇒ Area of track = π(632 – 562) (taking π common from R.H.S)
⇒ Area of track = π(3969 – 3136)
⇒ Area of track = π×833
= 22×119
= 2618 m2
The width of tack is 7 m and area of track is 2618 m2.
