The length of an arc of a circle, subtending an angle of 54° at the centre is 16.5 cm. Calculate the radius, circumference and area of the circle.
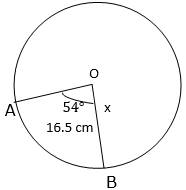
Consider the Circle shown above,
We know, Length of arc of sector![]()
Where R = radius of circle and θ = central angle of the sector
Given, Length of arc = ℓ = 16.5 cm and θ = 54o. Let the radius be x cm
Put the values of ℓ and θ in equation 1
![]()
![]()
![]()
On rearranging
![]()
![]()
⇒ x = 17.5 cm
Also, we know circumference of the circle = 2πR
⇒ Circumference of the circle = 2πx (put value of x in this equation)
⇒ Circumference of the circle = 2π(17.5)
![]()
![]()
![]()
⇒ Circumference of the circle = 110 cm
Also, we know Area of the circle = πR2
⇒ Area of the circle = πx2
⇒ Are of the circle = π(17.52)
![]()
![]()
![]()
⇒ Area of the circle = 962.5 cm2
The radius of circle is 17.5 cm, circumference is 110 cm and area is 962.5 cm2