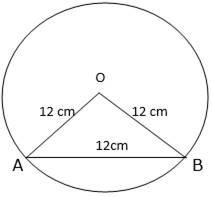
Consider the figure shown above.

In this, the triangle AOB is an equilateral triangle as all the sides are equal; therefore, it is obvious that the central angle of the sector is 60 degrees. Now by simply applying the formula of length of an arc, we can easily calculate the length of arc of the sector AOB.

Given Radius of circle = R = 12 cm,

Length of chord AB = 12 cm

∴ Central angle = θ = 60° (∵ ∆AOB is an equilateral triangle)

Where R = radius of the circle and θ = central angle of the sector

Put the values of R and θ in equation 1

= 2×3.14×2

= 12.56 cm

Now, Length of major arc = 2πR – Length of minor arc

⇒ Length of major arc = 2π(12) – 12.56 (put π = 3.14)

⇒ Length of major arc = (2×3.14×12) – 12.56

⇒ Length of major arc = 75.36 – 12.56

⇒ Length of major arc = 62.8 cm

Now, Area of minor segment = Area of sector – Area of triangle → eqn1

= 75.36 cm²→ eqn2

⇒ Area of triangle = 1.73×36

⇒ Area of triangle = 62.28 cm²→ eqn3

Put the values of equation 2 and 3 in equation 1,

∴ Area of minor segment = 75.36 – 62.28

= 13.08 cm²

Length of major arc is 62.8 cm and of minor arc is 12.56 cm and area of minor segment is 13.08 cm².