RS Aggarwal - Mathematics

Book: RS Aggarwal - Mathematics

Chapter: 18. Area of Circle, Sector and Segment

Subject: Maths - Class 10th

Q. No. 28 of Exercise 18B

Listen NCERT Audio Books to boost your productivity and retention power by 2X.

28

If a square is inscribed in a circle, find the ratio of the areas of the circle and the square.

Consider the figure shown below where O is centre of circle, join BC which passes through O, let the side of square be ‘a’ and radius of circle be ‘r’.


Now we know OB and OC are radius of circle


So, OB = OC = r



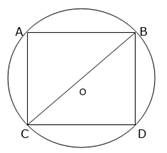
Consider ∆BDC right angled at D




And we know BC = OC + OB


BC = 2r and BD = DC = a (put these values in eqn1)


⇒ (2r)2 = a2 + a2


⇒ 4r2 = 2a2




Area of inscribed square = side × side


Areaa of inscribed square = a × a


Area of inscribed square = a2→ eqn3


Area of circumscribing circle = πR2 where R = radius of circle


⇒ Area of circumscribing circle = πr2→ eqn4



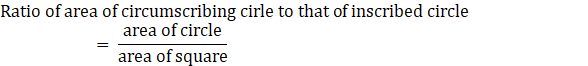
Put the values from equation 3 & 4 in above equation




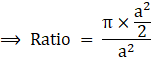
(from eqn 2)



So, Ratio is π : 2


The ratio is π:2


Chapter Exercises

Exercise 18A
Exercise 18B
Multiple Choice Questions (MCQ)
Formative Assessment (Unit Test)

More Exercise Questions

1

The circumference of a circle is 39.6 cm. Find its area.
2

The area of a circle is 98.56 cm2. Find its circumference.
3

The circumference of a circle exceeds its diameter by 45 cm. Find the circumference of the circle.
4

A copper wire when bent in the form of a square encloses an area of 484 cm2. The same wire is now bent in the form of a circle. Find the area enclosed by the circle.
5

A wire when bent in the form of an equilateral triangle endoses an area of 121√3 cm2. The same wire is bent to form a circle. Find the area enclosed by the circle.
6

The length of a chain used as the boundary of a semicircular park is 108 m. Find the area of the park.
7

The sum of the radii of two circles is 7 cm, and the difference of their circumferences is 8 cm. Find the circumferences of the circles.
8

Find the area of a ring whose outer and inner radii are respectively 23 cm and 12 cm.
9

A path of 8 m width runs around the outside of a circular park whose radius is 17 m. Find the area of the path.
10

A racetrack is in the form of a ring whose inner circumference is 352 m and outer circumference is 396 m. Find the width and the area of the track.
11

A sector is cut from a circle of radius 21 cm. The angle of the sector is 150°. Find the length of the arc and the area of the sector.
12

The area of the sector of a circle of radius 10.5 cm is 69.3 cm2. Find the central angle of the sector.
13

The length of an arc of a circle, subtending an angle of 54° at the centre is 16.5 cm. Calculate the radius, circumference and area of the circle.
14

The radius of a circle with centre O is 7 cm. Two radii OA and OB are drawn at right angles to each other. Find the areas of minor and major segments.
15

Find the lengths of the arcs cut off from a circle of radius 12 cm by a chord 12 cm long. Also, find the area of the minor segment. [Take π = 3.14 and √3 = 1.73.]
16

A chord 10 cm long is drawn in a circle whose radius is 5√2 cm. Find the areas of both the segments. [Take π = 3.14.]
17

Find the area of both the segments of a circle of radius 42 cm with central angle 120°. [Given, sin 120° = √3/2 and √3 = 1.73.]
18

A chord of a circle of radius 30 cm makes an angle of 60° at the centre of the circle. Find the areas of the minor and major segments. [Take π = 3.14 and √3 = 1.732.]
19

In a circle of radius 10.5 cm, the minor arc is one-fifth of the major arc. Find the area of the sector corresponding to the major arc.
20

The short and long hands of a clock are 4 cm and 6 cm long respectively. Find the sum of distances travelled by their tips in 2 days. [Take π = 3.14.]
21

Find the area of a quadrant of a circle whose circumference is 88 cm.
22

A rope by which a cow is tethered is increased from 16 m to 23 m. How much additional ground does it have now to graze?
23

A horse is placed for grazing inside a rectangular field 70 m by 52 m. It is tethered to one corner by a rope 21 m long. On how much area can it graze? How much area is left ungrazed?
24

A horse is tethered to one corner of a field which is in the shape of an equilateral triangle of side 12 m. If the length of the rope is 7 m, find the area of the field which the horse cannot graze. Take √3 = 1.732. Write the answer correct to 2 places of decimal.
25

Four cows are tethered at the four corners of a square field of side 50 m such that each can graze the maximum unshared area. What area will be left ungrazed? [Take π = 3.14.]
26

In the given figure, OPQR is a rhombus, three of whose vertices lie on a circle with centre O. If the area of the rhombus is 32√3 cm2, find the radius of the circle.
27

The side of a square is 10 cm. Find

(i) The area of the inscribed circle, and


(ii) The area of the circumscribed circle. [Take π = 3.14.]
28

If a square is inscribed in a circle, find the ratio of the areas of the circle and the square.
29

The area of a circle inscribed in an equilateral triangle is 154 cm2. Find the perimeter of the triangle. [Take √3 = 1.73.]
30

The radius of the wheel of a vehicle is 42 cm. How many revolutions will it complete in a 19.8-km-long journey?
31

The wheels of the locomotive of a train are 2.1 m in radius. They make 75 revolutions in one minute. Find the speed of the train in km per hour.
32

The wheels of a car make 2500 revolutions in covering a distance of 4.95 km. Find the diameter of a wheel.
33

A boy is cycling in such a way that the wheels of his bicycle are making 140 revolutions per minute. If the diameter of a wheel is 60 cm, calculate the speed (in km/h) at which the boy is cycling.
34

The diameter of the wheels of a bus is 140 cm. How many revolutions per minute do the wheels make when the bus is moving at a speed of 72.6 km per hour?
35

The diameters of the front and rear wheels of a tractor are 80 cm and 2 m respectively. Find the number of revolutions that a rear wheel makes to cover the distance which the front wheel covers in 800 revolutions.
36

Four equal circles are described about the four corners of a square so that each touches two of the others, as shown in the figure. Find the area of the shaded region, if each side of the square measures 14 cm.
37

Four equal circles, each of radius 5 cm, touch each other, as shown in the figure. Find the area included between them. [Take π = 3.14]
38

Four equal circles, each of radius a units, touch each other. Show that the area between them is sq units.
39

Three equal circles, each of radius 6 cm, touch one another as shown in the figure. Find the area enclosed between them. [Take π = 3.14 and √3 = 1.732.]
40

If three circles of radius a each, are drawn such that each touches the 4 other two, prove that the area included between them is equal to [Take √3 = 1.73 and π = 3.14.]
41

In the given figure, ABCD is a trapezium of area 24.5 cm2. If AD || BC, ∠DAB = 90°, AD = 10 cm, BC = 4 cm and ABE is quadrant of a circle then find the area of the shaded region.
42

ABCD is a field in the shape of a trapezium, AD || BC, ∠ABC = 90° and ∠ADC = 60°. Four sectors are formed with centres A, B, C and D, as shown in the figure. The radius of each sector is 14 m.


Find the following:


(i) total area of the four sectors,


(ii) area of the remaining portion, given that AD = 55 m, BC = 45 m and AB = 30 m.
43

Find the area of the shaded region in the given figure, where a circular arc of radius 6 cm has been drawn with vertex of an equilateral triangle of side 12 cm as centre and a sector of circle of radius 6 cm with centre B is made. [Use √3 = 1.73 and π = 3.14.]
44

In the given figure, ABCD is a rectangle with AB = 80 cm and BC = 70 cm, ∠AED = 90° and DE = 42 cm. A semicircle is drawn, taking BC as diameter. Find the area of the shaded region.
45

In the given figure, from a rectangular region ABCD with AB = 20 cm, a right triangle AED with AE = 9 cm and DE = 12 cm, is cut off. On the other end, taking BC as diameter, a semicircle is added on outside the region. Find the area of the shaded region. [Use π = 3.14.]
46

In the given figure, O is the centre of the circle with AC = 24 cm, AB = 7 cm and ∠BOD = 90°. Find the area of shaded region. [Use π = 3.14.]
47

In the given figure, a circle is inscribed in an equilateral triangle ABC of side 12 cm. Find the radius of inscribed circle and the area of the shaded region. [Use √3 = 1.73 and π = 3.14.]
48

On a circular table cover of radius 42 cm, a design is formed by a girl leaving an equilateral triangle ABC in the middle, as shown in the figure. Find the covered area of the design. [Use √3 = 1.73]
49

The perimeter of the quadrant of a circle is 25 cm. Find its area.
50

A chord of a circle of radius 10 cm subtends a right angle at the centre. Find the area of the minor segment. [Use π = 3.14.]
51

The radius of a circular garden is 100 m. There is a road 10 m wide, running all around it. Find the area of the road and the cost of levelling it at Rs. 20 per m2. [Use π = 3.14.]
52

The area of an equilateral triangle is 49√3 cm2. Taking each angular point as centre, circles are drawn with radius equal to half the length of the side of the triangle. Find the area of the triangle not included in the circles. [Take √3 = 1.73.]
53

A child draws the figure of an aeroplane as shown. Here, the wings ABCD and FGHI are parallelograms, the tail DEF is an isosceles triangle, the cockpit CKI is a semicircle and CDFI is a square. In the given figure, BP ⊥ CD, HQ ⊥ FI and EL ⊥ DF. If CD = 8 cm, BP = HQ = 4 cm and DE = EF = 5 cm, find the area of the whole figure. [Take π = 3.14.]
54

A circular disc of radius 6 cm is divided into three sectors with central angles 90°, 120° and 150°. What part of the whole circle is the sector with central angle150°? Also, calculate the ratio of the areas of the three sectors.
55

A round table cover has six equal designs as shown in the given figure. If the radius of the cover is 35 cm then find the total area of the design. [Use √3 = 1.732 and π = 3.14.]
56

In the given figure, PQ = 24 cm, PR = 7 cm and 0 is the centre of the circle. Find the area of the shaded region. [Take π = 3.14.]
57

In the given figure, ΔABC is right-angled at A. Find the area of the shaded region if AB = 6 cm, BC = 10 cm and 0 is the centre of the incircle of ΔABC. [Take π = 3.14.]
58

In the given figure, ΔABC is right-angled at A. Semicircles are drawn on AB, AC and BC as diameters. It is given that AB = 3 cm and AC = 4 cm. Find the area of the shaded region.
59

PQRS is a diameter of a circle of radius 6 cm. The lengths PQ, QR and RS are equal. Semicircles are drawn with PQ and QS as diameters, as shown in the given figure. If PS = 12 cm, find the perimeter and area of the shaded region. [Take π = 3.14.]
60

The inside perimeter of a running track shown in the figure is 400 m. The length of each of the straight portions is 90 m, and the ends are semicircles. If the track is 14 m wide everywhere, find the area of the track. Also, find the length of the outer boundary of the track.

Students Store