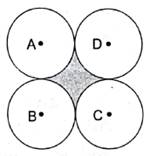
Here, first we join the center of all adjacent circles then the distance between the center of circles touching each other is equal to the side of the square formed by joining the center of adjacent circles. Therefore, we can say that the side of the square equal to the twice of the radius of circle. Now by simply calculating the area of the 4 quadrants and then subtracting it from the area of the square we can easily calculate the area of the shaded region.

Given radius of each circle = r = 5 cm

Central angle of each sector formed at corner = θ = 90°

Side of square ABCD = a = 2×r = 2×5 = 10 cm

where R = radius of circle

(putting value of r and θ)

Area of all 4 quadrants = 4×Area of one quadrant

⇒ Area of all 4 quadrants = 25π → eqn2

Area of square = side×side = a×a = a²

⇒ Area of square = 10² (putting value of side of square)

⇒ Area of square = 100 cm²→ eqn3

Area of shaded region = Area of square – Area of all 4 quadrants

Area of shaded region = 100 – 25π (from eqn3 and eqn2)

= 100 – (25×3.14) (put π = 3.14)

= 100 – 78.5

= 21.5 cm²

The area of shaded region is 21.5 cm².