In the given figure, ABCD is a trapezium of area 24.5 cm². If AD || BC, ∠DAB = 90°, AD = 10 cm, BC = 4 cm and ABE is quadrant of a circle then find the area of the shaded region.

Question

In the given figure, ABCD is a trapezium of area 24.5 cm 2 . If AD || BC, ∠ DAB = 90°, AD = 10 cm, BC = 4 cm and ABE is quadrant of a circle then find the area of the shaded region.

Philoid · Accepted Answer

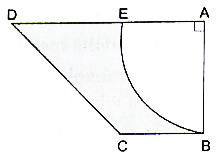
Here in order to find the area of the shaded region we have to calculate the area, or the quadrant shown and subtract it from the area of the trapezium. And in order to find the area of the quadrant we have to calculate the radius of the sector EAB by the area of trapezium.

Given Area of trapezium ABCD = 24.5 cm²→ eqn1

AD ∥ BC, AD = 10 cm, BC = 4 cm, ∠DAB = 90°

Putting the values in equation 2, we get,

⇒ AB = 3.5 cm

Therefore radius of the sector EAB = r = 3.5 cm

⇒ Area of the quadrant EAB = 9.625 cm²→ eqn3

∴ Area of shaded region = Area of trapezium – Area of quadrant EAB

⇒ Area of shaded region = 24.5 – 9.625 (putting values from eqn1 and eqn3)

⇒ Area of shaded region = 14.875 cm²

Area of the shaded region = 14.875 cm².

In the given figure, ABCD is a trapezium of area 24.5 cm2. If AD || BC, ∠DAB = 90°, AD = 10 cm, BC = 4 cm and ABE is quadrant of a circle then find the area of the shaded region.

In the given figure, ABCD is a trapezium of area 24.5 cm². If AD || BC, ∠DAB = 90°, AD = 10 cm, BC = 4 cm and ABE is quadrant of a circle then find the area of the shaded region.