ABCD is a field in the shape of a trapezium, AD || BC, ∠ABC = 90° and ∠ADC = 60°. Four sectors are formed with centres A, B, C and D, as shown in the figure. The radius of each sector is 14 m.
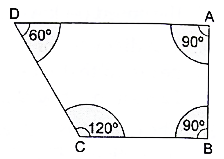
Find the following:
(i) total area of the four sectors,
(ii) area of the remaining portion, given that AD = 55 m, BC = 45 m and AB = 30 m.
Here in order to find the area of the shaded region we have to calculate the area, or the quadrant shown and subtract it from the area of the trapezium. And in order to find the area of the quadrant we have to calculate the radius of the sector EAB by the area of trapezium.
Given AB = 30 m, AD = 55 m, BC = 45 m
θA = 90°, θB = 90°, θC = 120°, θD = 60°
Radius of each sector = r = 14 m
(i) total area of 4 sectors
![]()
![]()
![]()
![]()
Area of sector at corner A = 49π m2→ eqn2
As we know that central angle at A and B are both 90 degrees and radius is also same i.e. 14 m therefore the area of the sector at B will be exactly same as that of sector at A.
∴ Area of sector at corner B = Area of sector at corner A
⇒ Area of sector at corner B = 49π → eqn3
Similarly,
![]()
![]()
![]()
Area of sector at corner C = 65.33π m2→ eqn4
Similarly,
![]()
![]()
![]()
Area of sector at corner D = 32.67π → eqn5
Total area of 4 sectors = eqn2 + eqn3 + eqn4 + eqn5
⇒ Total area of 4 sectors = 49π + 49π + 65.33π + 32.67π
⇒ Total area of 4 sectors = 196π
![]()
![]()
∴ Total area of 4 sectors = 616 m2
Total area of 4 sectors is 616 m2.
(ii) Area of the remaining portion
Here in order to find the area of the remaining portion of the trapezium we have to subtract the area of the 4 sectors from the area of the trapezium.
![]()
![]()
On putting the values,
Area of trapezium![]()
![]()
= 50×30
Area of trapezium = 1500 m2→ eqn1
Area of remaining portion = Area of trapezium – Area of the 4 sectors
⇒ Area of remaining portion = 1500 – 616 (from eqn1 and part (i))
∴ Area of remaining portion = 884 m2
The area of the remaining portion is 884 m2.