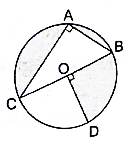
Here in order to find the area of the shaded region (region excluding the area of segment AC and quadrant OCD) can be calculated by subtracting the area of triangle and quadrant OBD from the area of the circle.

Given AC = 24 cm, AB = 7 cm and ∠BOD = 90°

Here we see that the triangle ACB is right angle triangle, therefore, we can apply Pythagoras theorem i.e.

BC² = AC² + AB²

⇒ BC² = 24² + 7² (putting the given values)

⇒ BC² = 576 + 49

⇒ BC² = 625

BC = √625

∴ BC = 25 cm

Area of ∆ACB = 1/2×AB×AC (Area of triangle = 1/2×base×height)

On putting values we get,

⇒ Area of ∆AED = 7×12

∴ Area of ∆AED = 84 cm²→ eqn1

Area of circle = πR² (R = radius of circle)

⇒ R = 12.5 cm

∴ Area of circle = π× 12.5²

⇒ Area of circle = 156.25×3.14 (put π = 3.14)

∴ Are of circle = 490.625 cm²→ eqn2

⇒ Area of quadrant OBD = 122.65625 cm²→ eqn3

Area of shaded region = Area of circle – Area of quadrant – Area of ∆

⇒ Area of shaded region = 490.625 – 84 – 122.65625 (from eqn1, 2 and 3)

⇒ Area of shaded region = 283.96875 cm²

Area of shaded region is 283.96875 cm².