In the given figure, a circle is inscribed in an equilateral triangle ABC of side 12 cm. Find the radius of inscribed circle and the area of the shaded region. [Use √3 = 1.73 and π = 3.14.]

Here we will draw median from all the vertices of the equilateral triangle and the point at which they intersect will be the incircle of the triangle and that will be the centre of the circle. Thenwith the help of which we will find out the height of the triangle and subsequently the radius of the circle and ultimately the area of the shaded region (region of equilateral triangle excluding the area of circle inscribed).
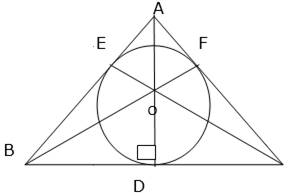
As AD = BF = CE = h
Consider ∆ADB, ∠ADB = 90°, BD = 6 cm
![]()
122 = AD2 + 62 (putting the given values)
144 = AD2 + 36
144 – 36 = AD2
AD2 = 108
![]()
![]()
![]()
![]()
We also know that a point O will divide each median in a ratio of 2:1
![]()
![]()
![]()
![]()
Area of the circle = πr2
![]()
∴ Area of the circle = 12π cm2→ eqn1
![]()
![]()
![]()
![]()
Area of shaded region = area of triangle – area of circle
![]()
⇒ Area of the shaded region = (36×1.73) – (12×3.14)
⇒ Area of the shaded region = 62.28 -37.68
∴ Area of the shaded region = 24.6 cm2
![]()