On a circular table cover of radius 42 cm, a design is formed by a girl leaving an equilateral triangle ABC in the middle, as shown in the figure. Find the covered area of the design. [Use √3 = 1.73]
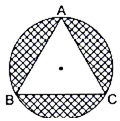
Here we will first find the sides of equilateral triangle ant then subtract the area of the triangle from the area of the circle.
Given radius of circle = r = 42 cm
∴ Area of the circle = πR2, where R = radius of the circle
⇒ Area of the circle = π(422)
![]()
⇒ Area of the circle = 22×252
∴ Area of the circle = 5544 cm2→ eqn1
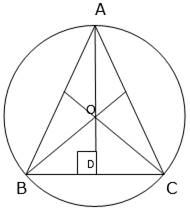
Consider the figure shown,
In ∆ABD, ∠ADB = 90°
![]()
Let the sides of the equilateral triangle = a cm
And as we know AD is a median therefore it will bisect the side BC into two equal parts i.e.
BD = DC → eqn3
Also, BC = BD + DC
⇒ BC = BD + BD (from eqn3)
⇒ a = 2BD (BC = a)
![]()
![]()
![]()
![]()
![]()
![]()
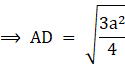
![]()
Now, we also know that the point ‘O’ which is the intersection of all the three medians i.e. centroid of the triangle. Also we know that the centroid divides the median in the ratio 2:1.
![]()
Also, we know AO = radius = r = 42 cm
![]()
![]()
⇒ AD = 63 cm
Putting the value in equation 4,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Area of covered by design = Area of circle – Area of triangle ABC
![]()
![]()
⇒ Area covered by design = 5544 – 2288.79
∴ Area covered by design = 3255.21 cm2
Area covered by design is 3255.21 cm2.