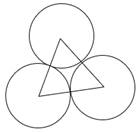
The area of an equilateral triangle is 49√3 cm 2 . Taking each angular point as centre, circles are drawn with radius equal to half the length of the side of the triangle. Find the area of the triangle not included in the circles. [Take √3 = 1.73.]

Question

Philoid · Accepted Answer

Each angle of triangle = θ = 60°

Area of triangle not included in circles = Area of triangle – Area of all sectors

Area of all 3 sectors area equal as all the three circles are having same radius which is equal to the half of the side of the equilateral triangle.

Let the side of equilateral triangle be = a cm

⇒ a = 7×2

⇒ a = 14 cm

So radius of the circles = 7 cm

∴ Area of all 3 sectors = 77 cm²→ eqn1

Area of triangle not included = (49×1.73) - 77

⇒ Area of triangle not included = 84.77 – 77

∴ Area of triangle not included = 7.77 cm²

Area of triangle not included in circles is 7.77 cm².

The area of an equilateral triangle is 49√3 cm2. Taking each angular point as centre, circles are drawn with radius equal to half the length of the side of the triangle. Find the area of the triangle not included in the circles. [Take √3 = 1.73.]

The area of an equilateral triangle is 49√3 cm². Taking each angular point as centre, circles are drawn with radius equal to half the length of the side of the triangle. Find the area of the triangle not included in the circles. [Take √3 = 1.73.]