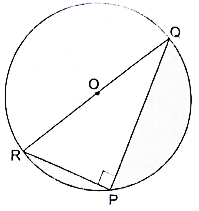
Here we will subtract the area of right angle triangle PQR and semicircle from the area of entire circle.

Given PQ = 24 cm, PR = 7 cm

Consider ∆PQR, ∠QPR = 90°

RQ² = 24² + 7²

⇒ RQ² = 576 + 49

⇒ RQ² = 625

Therefore Radius of the circle = half of RQ

Let radius be ‘r’

∴ r = 12.5 cm

Area of ∆PQR = 7×12

∴ Area of ∆PQR = 84 cm²→ eqn1

∴ Area of semicircle = 245.3125 cm²→ eqn2

Area of circle = πr²

Area of circle = π(12.5²)

⇒ Area of circle = 3.14×156.25 (putting π = 3.14)

∴ Area of circle = 490.625 cm²→ eqn3

Area of shaded region = eqn3 – eqn2 – eqn1

⇒ Area of shaded region = 490.625 – 245.3125 – 84

∴ Area of shaded region = 161.3125 cm²

Area of shaded region is 161.3125 cm².