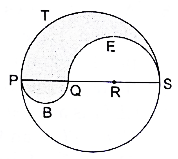
Here we will subtract the area of semicircle whose diameter is QS from the area of the semicircle whose diameter PS and add the area of semicircle whose diameter is PQ so as to find out the area of the shaded region.

Given PS = 12 cm

Radius of the circle = 6 cm

PQ = QR = RS

So let PQ = QR = RS = k cm

Also, PQ + QR + RS = PS

⇒ k + k + k = 12

⇒ 3k = 12

∴ k = 4 cm

So, PQ = QR = RS = 4 cm

Area and perimeter of semicircle whose diameter is PS

∴ Radius = 6 cm

∴ Area of semicircle = 18π cm²→ eqn2

Perimeter of semicircle = πr

⇒ Perimeter of semicircle = π×6

∴ Perimeter of semicircle = 6π cm → eqn3

Area of semicircle whose diameter is QS

⇒ Radius = 4 cm

∴ Area of semicircle = 8π cm²→ eqn4

Perimeter of semicircle = πr

⇒ Perimeter of semicircle = π×4

∴ Perimeter of semicircle = 4π cm → eqn5

Area of semicircle whose diameter is PQ

∴ Radius = 2 cm

∴ Area of semicircle = 2π cm²→ eqn6

Perimeter of semicircle = πr

⇒ Perimeter of semicircle = π×2

∴ Perimeter of semicircle = 2π cm → eqn7

Area of the shaded region = eqn2 – eqn4 + eqn6

Area of shaded region = 18π – 8π + 2π

⇒ Area of shaded region = 12π

⇒ Area of shaded region = 12×3.14 (putting π = 3.14)

∴ Area of shaded region = 37.68 cm²

Perimeter of shaded region = eqn3 – eqn5 + eqn7

⇒ Perimeter of shaded region = 6π -4π + 2π

⇒ Perimeter of shaded region = 4π

⇒ Perimeter of shaded region = 4×3.14 (put π = 3.14)

∴ Perimeter of shaded region = 12.56 cm

Perimeter of the shaded region is 12.56 cm and Area of shaded region is 37.68 cm².