OACB is a quadrant of a circle with centre O and its radius is 3.5 cm. If OD = 2 cm, find the area of (i) the quadrant OACB
(ii) the shaded region. [Take π = 22/7]
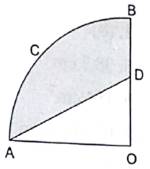
Radius of circle = R = 3.5 cm
OD = 2 cm
OA = OB = R = 3.5 cm
Since, OACB is a quadrant of a circle ∴ angle subtended by it at the centre = 90°
(i) Area of quadrant = ![]()
= 22/7 × 3.5 × 3.5 × 90°/360° cm2
= 9.625 cm2
(ii) Area of shaded region = Area of quadrant – Area of triangle OAD
Area of triangle OAD = 1/2 × base × height
= 1/2 × OA × OD
= 1/2 × 3.5 × 2 cm2
= 3.5 cm2
Area of shaded region = 9.625 cm2 – 3.5cm2
= 6.125 cm2
13