A chord of a circle of radius 30 cm makes an angle of 60° at the centre of the circle. Find the areas of the minor and major segments. [Take π = 22/7 and √3 = 1.732.]
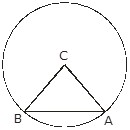
∠ACB = 60°
Chord AB subtends an angle of 60° at the centre
Radius = 30 cm
Let Radius be R
In triangle ABC, AC = BC
So, ∠CAB = ∠CBA
∠ ACB + ∠ CAB + ∠ CBA = 180°
60° + 2∠CAB = 180°
2∠CAB = 180° - 60° = 120°
∠CAB = 120°/2 = 60°
∠CAB = ∠CBA = 60°
∴ ΔABC is a equilateral triangle
Length of side of an equilateral triangle = radius of circle = 30 cm
Area of equilateral triangle = √3/4 × side2 = 1.732/4 × 30 × 30 cm2
= 389.7 cm2
Area of sector ACB = ![]() = 3.14 × 30 × 30 × 60°/360° = 471.45 cm2
= 3.14 × 30 × 30 × 60°/360° = 471.45 cm2
Area of minor Segment = Area of sector ACB – Area of ΔABC
= 471.45 cm2 – 389.7 cm2 = 81.75 cm2
Area of circle = ![]() R2 = 3.14 × 30 × 30 cm2 = 2828.57 cm2
R2 = 3.14 × 30 × 30 cm2 = 2828.57 cm2
Area of major segment = Area of circle – Area of minor segment
= 2826 cm2 – 81.75 cm2
= 2744.25 cm2