Four cows are tethered at the four corners of a square field of side 50 m such that each can graze the maximum unshared area. What area will be left ungrazed? [Take π = 3.14]
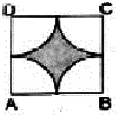
From the figure we see that cows are tethered at the corners of the square so while grazing they form four quadrants as shown in the figure
Length of side of square = 50 m
Length of side of square = 2 × Radius of quadrant
Radius of quadrant = R = 50/2 m
= 25 m
Area of square = side2
= 502 m2 = 2500 m2
Area of quadrant = 1/4 π R2 = 1/4 × 3.14 × 25 × 25 m2
= 490.625 m2
Area of 4 quadrants = 4 × 490.625 m2
= 1962.5 m2
Area left ungrazed = Area of shaded part
= Area of square – Area of 4 quadrants
= 2500 m2 – 1962.5 m2
= 537.5 m2
19