An observer 1.5 m tall is 30 m away from a chimney. The angle of elevation of the top of the chimney from his eye is 60°. Find the height of the chimney.

Question

Philoid · Accepted Answer

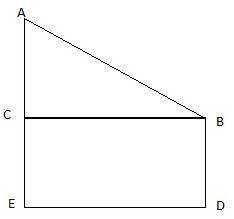
In the figure, let BD be the height of the man, i.e. BD = 1.5m. Let AE be the chimney in the figure. Join B and C. We get a triangle which is right angled at C. Clearly, BD = CE. Also, given that ∠ ABC = 60°. We use the trigonometric ratio tan which uses AC as height and BC as a base to find the height of the chimney AE.

Now, clearly CE = 1.5m. The height of the chimney is AE.

From ∆ABC,

or,

Thus, AC = 51.96m and CE = 1.5m. The height of the chimney

AE = AC + CE = 51.96 + 1.5 = 53.46 m.

Hence, the answer is 53.46 m.