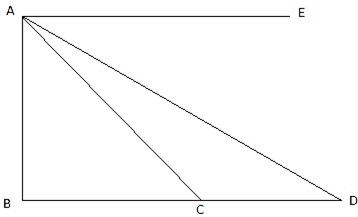
Let AB be the hill and C, D are the km stones. Join B, C, D. Also join C, D with A. So we get two right-angled triangles ABC and ABD with right angle at B. Draw a line AE parallel to BD. Given that the angles of depression of C and D are 45° and 30° respectively. So, ∠EAD = ∠ADB = 30° and ∠EAC = ∠ACB = 45°. Now, CD = 1km. We are to find the height of the hill, that is, AB.

In ∆ABC,

or,

In ∆ABD,

or,

or,

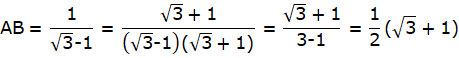
So, the correct option is (B).