Integrate the functions.
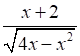
Let x + 2 = ![]()
⇒ x + 2 = A(4 -2x) + B
Now, equating the coefficients of x and constant term on both sides, we get,
-2A = 1
⇒ A = ![]()
4A + B = 2
⇒ B = 4
⇒ x + 2 = ![]()
Now, 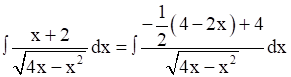
⇒ 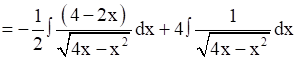
Now, let us consider, 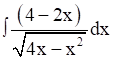
Let 4x – x2 = t
⇒ (4 -2x) dx= dt
 …(1)
…(1)
And, Now let us consider, 
Then, 4x – x2 = -(-4x + x2)
= (-4x + x2 + 4 – 4)
= 4 – (x - 2)2
= (2)2 – (x - 2)2
 …(2)
…(2)
using eq. (1) and (2), we get,
⇒ 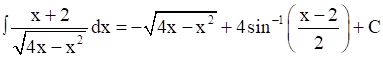
21