Integrate the rational functions.
![]()
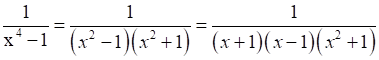
Let 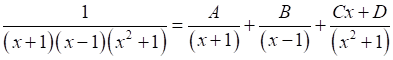
1 = A(x-1)(x2+1) + B(x+1)(x2+1) + (Cx + D)(x2 - 1)
1 = A(x3 + x – x2 -1) + B(x3 + x + x2 + 1) + Cx3 + Dx2 - Cx - D
1 = (A + B + C)x3 + (-A + B + D)x2 + (A + B - C)x + (-A + B - D)
Equating the coefficients of x3, x2, x and constant term, we get,
(A + B + C) = 0
(-A + B + C) = 0
(A + B - C) = 0
(-A + B - D) = 0
On solving these equations, we get,
A = ![]()
Therefore,
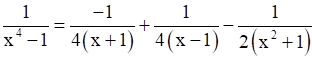
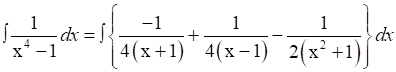
![]()
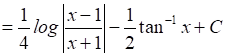
17