Integrate the rational functions.
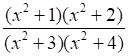
Now, 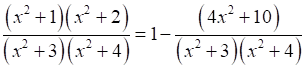
Let 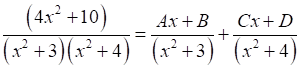
4x2 + 10 = (Ax + B)(x2 + 4) + (Cx + D)(x2 + 3)
⇒ 4x2 + 10 = Ax3 + 4Ax + Bx2 + 4B + Cx3 + 3Cx + Dx2 + 3D
⇒ 4x2 + 10 = (A+C)x3 + (B + D)x2 + (4A + 3C)x + (4B + 3D)
Equating the coefficients of x3, x2, x and constant term, we get,
A + C = 0
B + D = 0
4A + 3C = 0
4B + 3 B = 0
On solving these equations, we get,
A = 0, B = -2, C = 0 and D = 6
Therefore,
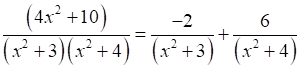
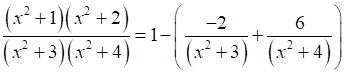
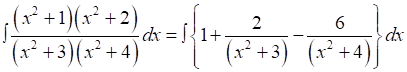
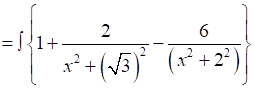
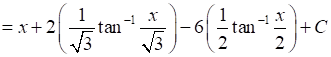
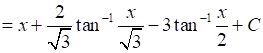
20