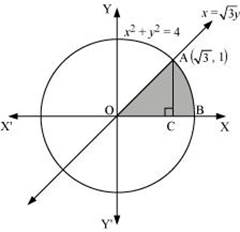
Find the area of the region in the first quadrant enclosed by x-axis, line ![]() and the circle x2 + y2 = 4.
and the circle x2 + y2 = 4.
The equations are ![]() and the circle
and the circle ![]()
From the figure we can see that the x-axis is the area OAB and it si shown by shaded region.
Now, the point of intersection of the line and the circle in the first quadrant is ![]() .
.
Area OAB = Area ΔOCA + Area ACB
Area of ΔOCA = 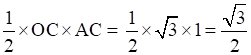
Also,
Area of ABC = 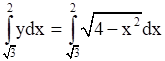
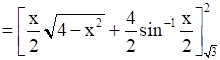
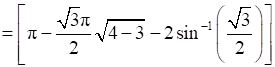
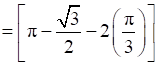
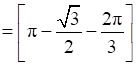
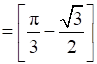
Therefore, required area is = 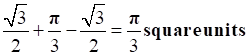 .
.
7