Find the area of the region bounded by the parabola y = x2 and y=|x|.
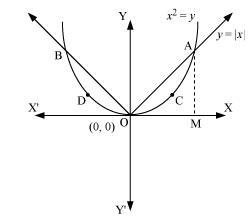
It is given that the area of the region bounded by the parabola y = x2 and y = |x|.
Now, we can observed that the given area is symmetrical about y-axis.
⇒ Area OACO = Area ODBO
And the point of intersection of parabola, y = x2 and y = x is A (1, 1).
Thus, Area OACO = Area ΔOAM – Area OMACO
Now, Area of ΔOAM = ![]()
Area of OMACO = 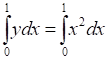
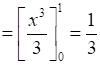
⇒ Area OACO = Area ΔOAM – Area OMACO
= ![]()
Therefore, the required area is 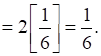
10