Mathematics Part-II

Book: Mathematics Part-II

Chapter: 8. Application of Integrals

Subject: Maths - Class 12th

Q. No. 10 of Exercise 8.1

Listen NCERT Audio Books - Kitabein Ab Bolengi

10

Find the area bounded by the curve x2 = 4y and the line x = 4y – 2.


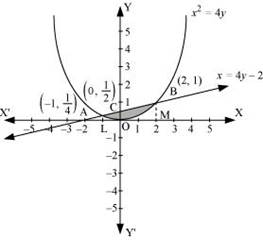
It is given that the area of the region bounded by the parabola x2 = 4y and x = 4y - 2.


Let A and B be the points of intersection of the line and parabola.


Coordinates of point A are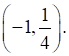


Coordinates of point B are (2, 1).


Now, draw AL and BM perpendicular to x axis.


We can see that


Area OBAO = Area OBCO + Area OAC) …(1)


Now, Area OBCA = Area OMBC – Area of OMBO




.




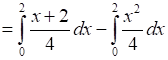
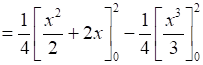
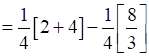Similarly,


Area OACO = Area OLAC – Area of OLAO







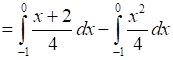
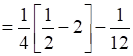
Therefore, the required area is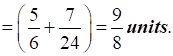


10

Chapter Exercises

Exercise 8.1
Exercise 8.2
Miscellaneous Exercise

More Exercise Questions

1

Find the area of the region bounded by the curve y2 = x and the lines x = 1, x = 4 and the x-axis in the first quadrant.
2

Find the area of the region bounded by y2 = 9x, x = 2, x = 4 and the x-axis in the first quadrant.
3

Find the area of the region bounded by x2 = 4y, y = 2, y = 4 and the y-axis in the first quadrant.
4

Find the area of the region bounded by the ellipse

5

Find the area of the region bounded by the ellipse

6

Find the area of the region in the first quadrant enclosed by x-axis, line and the circle x2 + y2 = 4.
7

Find the area of the smaller part of the circle x2 + y2 = a2 cut off by the line

8

The area between x = y2 and x = 4 is divided into two equal parts by the line x = a, find the value of a.
9

Find the area of the region bounded by the parabola y = x2 and y=|x|.
10

Find the area bounded by the curve x2 = 4y and the line x = 4y – 2.
11

Find the area of the region bounded by the curve y2 = 4x and the line x = 3.
12

Area lying in the first quadrant and bounded by the circle x2 + y2 = 4 and the lines x = 0 and x = 2 is
13

Area of the region bounded by the curve y2 = 4x, y-axis and the line y = 3 is