Find the area bounded by curves (x – 1)2 + y2 = 1 and x2 + y2 = 1.
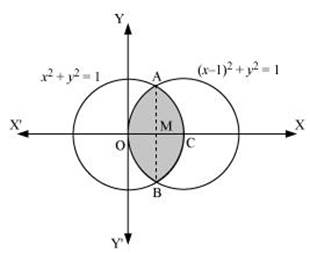
It is given that area of circle, (x – 1)2 + y2 = 1 and x2 + y2 = 1.
On solving the above two equations, we get the point of intersection
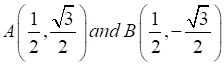
We can see that the required area is symmetrical about x axis.
Thus, Area OBCAO = 2 × Area OCAO
Let us draw AM perpendicular to OC.
⇒ The coordinates of M are (![]() , 0).
, 0).
Then, Area OCAO = Area OMAO + Area MCAM
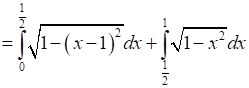
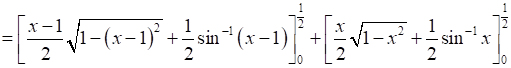
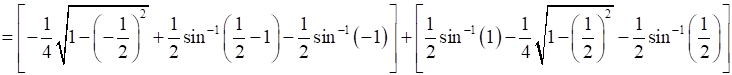
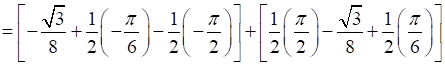
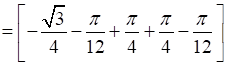
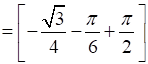
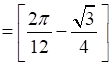
Therefore, the required area OBCAO 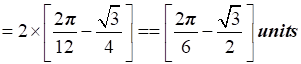
3