Find the area enclosed by the parabola 4y = 3x2 and the line 2y = 3x + 12.
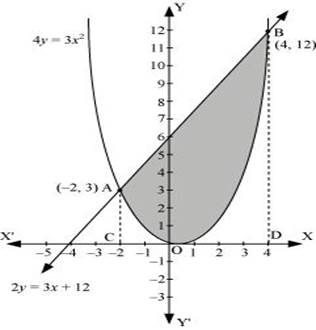
We can see from the figure that the area of the region bounded by the curve 4y = 3x2 and the line 2y = 3x + 12 is shown by shaded region that is Area OBAO.
The points of intersection of both the curves are A(-2,3) and (4, 12).
Now draw AC and BD perpendicular to x – axis.
Thus,
Area of OBAO = Area CDBA – (Area ODBA + Area OACO)
⇒ 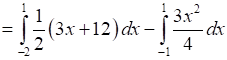
⇒ 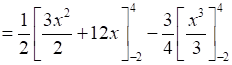
⇒ ![]()
⇒ ![]()
= 45 -18
= 27 units.
7