Using the method of integration find the area bounded by the curve |x| + |y| = 1. [ Hint: The required region is bounded by lines x + y = 1, x– y = 1, – x + y = 1 and – x – y = 1].

Question

Philoid · Accepted Answer

We can see from the figure that the area bounded by the curve |x| + |y| = 1 is shown by shaded region that is Area OACO.

The curve intersects the axes at points A(0,1), B(1,0), C(0,-1) and D(-1,0).

We can observed that the given curve is symmetrical about x-axis and y –axis.

Thus,

Area ADCB = 4 × Area OBAO

⇒

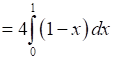
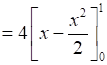
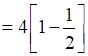
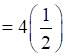
= 2 units

Using the method of integration find the area bounded by the curve |x| + |y| = 1.[Hint: The required region is bounded by lines x + y = 1, x– y = 1, – x + y = 1 and – x – y = 1].

Using the method of integration find the area bounded by the curve |x| + |y| = 1.
[Hint: The required region is bounded by lines x + y = 1, x– y = 1, – x + y = 1 and – x – y = 1].