Mathematics Part-II

Book: Mathematics Part-II

Chapter: 8. Application of Integrals

Subject: Maths - Class 12th

Q. No. 15 of Miscellaneous Exercise

Listen NCERT Audio Books - Kitabein Ab Bolengi

15

Find the area of the region {(x, y) : y2 ≤ 4x, 4x2 + 4y2 ≤ 9}


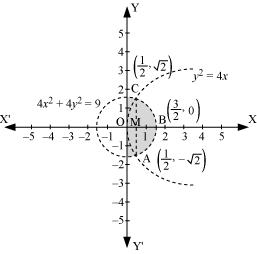
The area bounded by the curves, {(x, y) : y2 ≤ 4x, 4x2 + 4y2 ≤ 9}, is shown by shaded region as OABCO.


The points of intersection of both the curves are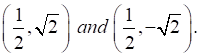


We can observed that area OABCO is symmetrical about x-axis.


Thus, Area of OABCO = 2 × Area OBC


Now,


Area OBCO = Area OMC + Area MBC


⇒


⇒


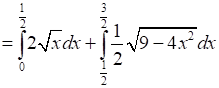
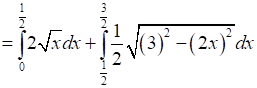
Put 2x = t


⇒ dx =


So, when x = , t = 3 and x = , t = 1, we get,


⇒


⇒


⇒


⇒


⇒


⇒


⇒


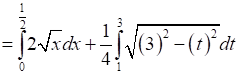
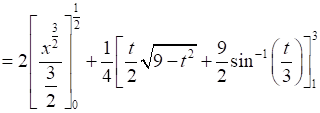
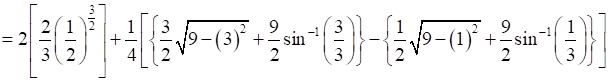
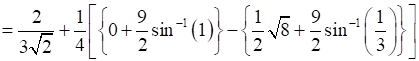
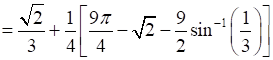
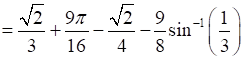
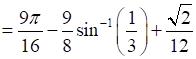
Therefore, the required area is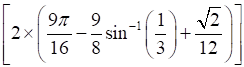



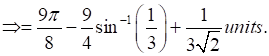
15

Chapter Exercises

Exercise 8.1
Exercise 8.2
Miscellaneous Exercise

More Exercise Questions

1

Find the area under the given curves and given lines:

y = x2, x = 1, x = 2 and x-axis
1

Find the area under the given curves and given lines:

y = x4, x = 1, x = 5 and x-axis
2

Find the area between the curves y = x and y = x2.
3

Find the area of the region lying in the first quadrant and bounded by y = 4x2, x = 0, y = 1 and y = 4.
4

Sketch the graph of y = |x+3| and evaluate

5

Find the area bounded by the curve y = sin x between x = 0 and x = 2π.
6

Find the area enclosed between the parabola y2 = 4ax and the line y = mx.
7

Find the area enclosed by the parabola 4y = 3x2 and the line 2y = 3x + 12.
8

Find the area of the smaller region bounded by the ellipse and the line

9

Find the area of the smaller region bounded by the ellipse line

10

Find the area of the region enclosed by the parabola x2 = y, the line y = x + 2 and the x-axis.
11

Using the method of integration find the area bounded by the curve |x| + |y| = 1.

[Hint: The required region is bounded by lines x + y = 1, x– y = 1, – x + y = 1 and – x – y = 1].
12

Find the area bounded by curves {(x, y): y ≥ x2 and y = |x|}.
13

Using the method of integration find the area of the triangle ABC, coordinates of whose vertices are A(2, 0), B (4, 5) and C (6, 3).
14

Using the method of integration find the area of the region bounded by lines:

2x + y = 4, 3x – 2y = 6 and x – 3y + 5 = 0
15

Find the area of the region {(x, y) : y2 ≤ 4x, 4x2 + 4y2 ≤ 9}
16

Area bounded by the curve y = x3, the x-axis and the ordinates x = – 2 and x = 1 is
17

The area bounded by the curve y = x |x|, x-axis and the ordinates x = – 1 and x = 1 is given by

[Hint: y = x2 if x > 0 and y = – x2 if x < 0].
18

The area of the circle x2 + y2 = 16 exterior to the parabola y2 = 6x is
19

The area bounded by the y-axis, y = cos x and y = sin x when is