If a line makes angles 90°, 135°, 45° with the x, y and z-axes respectively, find its direction cosines.
Let the direction cosines of the line making ∠ α with x-axis, β – with y axis and γ- with z axis are l, m and n
⇒ l = cos α, m = cos β and n = cos γ
Here α = 90°, β = 135° and γ = 45°
So direction cosines are
l = cos 90° = 0
m = cos 135°= cos (180° - 45°) = -cos 45° = 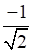
n = cos 45° = 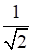
⇒ Direction cosines of the line 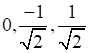
7