If the direction ratios of two lines segments are proportional, then the lines are collinear.

Given A(2, 3, 4), B(−1, −2, 1), C(5, 8, 7)

Direction ratio of line joining A (2,3,4) and B (−1, −2, 1), are

(−1−2), (−2−3), (1−4)

= (−3, −5, −3)

So a₁ = -3, b₁ = -5, c₁ = -3

Direction ratio of line joining B (−1, −2, 1) and C (5, 8, 7) are

(5− (−1)), (8−(−2)), (7−1)

= (6, 10, 6)

So a₂ = 6, b₂ = 10 and c₂ =6

It is clear that the direction ratios of AB and BC are of same proportions

As

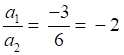
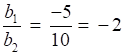
and

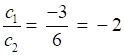
Therefore A, B, C are collinear.