Book: Mathematics Part-II
Chapter: 11. Three Dimensional Geometry
Subject: Maths - Class 12th
Q. No. 1 of Exercise 11.2
Listen NCERT Audio Books - Kitabein Ab Bolengi
Show that the three lines with direction cosines 
are mutually perpendicular.
We know that
If l1, m1, n1 and l2, m2, n2 are the direction cosines of two lines; and θ is the acute angle between the two lines; then cos θ = |l1l2 + m1m2 + n1n2|
If two lines are perpendicular, then the angle between the two is θ = 90°
⇒ For perpendicular lines, | l1l2 + m1m2 + n1n2 | = cos 90° = 0, i.e.
| l1l2 + m1m2 + n1n2 | = 0
So, in order to check if the three lines are mutually perpendicular, we compute | l1l2 + m1m2 + n1n2 | for all the pairs of the three lines.
Now let the direction cosines of L1, L2 and L3 be l1, m1, n1; l2, m2, n2 and l3, m3, n3.
First, consider
⇒ 
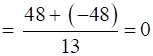
⇒ L1⊥ L2 ……(i)
Next, consider
⇒ 
⇒ 
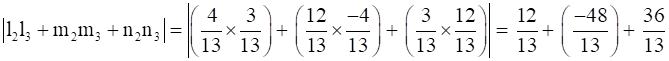
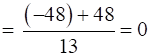
⇒ L2⊥ L3 …(ii)
Now, consider
⇒ 
⇒ 
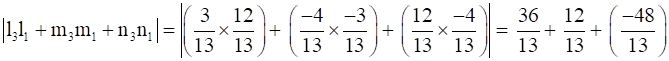
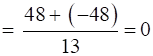
⇒ L1⊥ L3 …(iii)
∴ By (i), (ii) and (iii), we have
L1, L2 and L3 are mutually perpendicular.
