Find the equation of the plane through the line of intersection of the planes x + y + z = 1 and 2x + 3y + 4z = 5 which is perpendicular to the plane x – y + z = 0.

Question

Philoid · Accepted Answer

Let the eq. of the plane that passes through the two-given plane x + y + z = 1 and 2x + 3y + 4z = 5 is

(x + y + z – 1) + λ(2x + 3y + 4z – 5) = 0

(2λ + 1)x + (3λ + 1)y + (4λ + 1)z -1 - 5λ = 0 (i)

Direction ratio of the plane (2λ + 1, 3λ + 1, 4λ + 1)

and Direction ratio of another plane (1, -1, 1)

∵ Both are ⊥ hence

(2λ + 1 × 1) + (3λ + 1 × (-1)) + (4λ + 1 × 1) = 0

2λ + 1 - 3λ - 1 + 4λ + 1 = 0

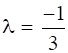
Put the value of λ in (i)eq., we get

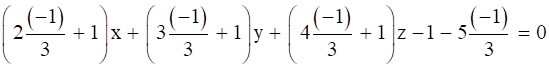
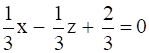
x – z + 2 = 0

This is the required eq. of the plane.