In each of the question verify that the given functions (explicit or implicit) is a solution of the corresponding differential equation:

Question

In each of the question verify that the given functions (explicit or implicit) is a solution of the corresponding differential equation: x + y = tan –1 y : y 2 y′ + y 2 + 1 = 0

Philoid · Accepted Answer

It is given that x + y = tan^-1y

Now, differentiating both sides w.r.t. x, we get,

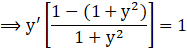
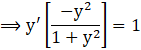
Now, Substituting the values of y’ in the given differential equations, we get,

LHS = y²y’ + y² + 1 =

= -1 – y² + y² + 1

= 0 = RHS

Therefore, the given function is the solution of the corresponding differential equation.

In each of the question verify that the given functions (explicit or implicit) is a solution of the corresponding differential equation:x + y = tan–1y : y2y′ + y2 + 1 = 0

In each of the question verify that the given functions (explicit or implicit) is a solution of the corresponding differential equation:
x + y = tan^–1y : y²y′ + y² + 1 = 0