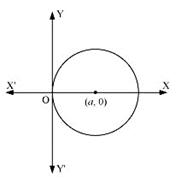
The center of the circle touching the y- axis at orgin lies on the x – axis.

Let (a,0) be the centre of the circle.

Thus, it touches the y – axis at orgin, its radius is a.

Now, the equation of the circle with centre (a,0) and radius (a) is

(x –a)² – y² = a²

⇒ x² + y² = 2ax

Now, differentiating both sides w.r.t. x , we get,

2x + 2yy’ = 2a

⇒ x + yy’ = a

Now, on substituting the value of a in the equation, we get,

x² + y² = 2(x + yy’)x

⇒ 2xyy’ + x² = y²

Therefore, the required differential equation is 2xyy’ + x² = y² .