For each of the differential equations in question, find the particular solution satisfying the given condition: 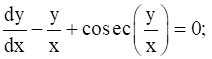y = 0 when x = 1

Mathematics Part-II

Book: Mathematics Part-II

Chapter: 9. Differential Equations

Subject: Maths - Class 12^th

Q. No. 14 of Exercise 9.5

Listen NCERT Audio Books - Kitabein Ab Bolengi

14

For each of the differential equations in question, find the particular solution satisfying the given condition:
y = 0 when x = 1

Here, putting x= kx and y = ky

= k⁰.f(x,y)

Therefore, the given differential equation is homogeneous.

To solve it we make the substitution.

y = vx

Differentiating eq. with respect to x, we get

Integrating both sides, we get

- cosv = - logx + C

y = 0 when x = 1

- 1 = C

The required solution of the differential equation.

14

Chapter Exercises

Exercise 9.1

Exercise 9.2

Exercise 9.3

Exercise 9.4

Exercise 9.5

Exercise 9.6

Miscellaneous Exercise

1

In each of the question, show that the given differential equation is homogeneous and solve each of them.
(x² + xy)dy = (x² + y²)dx

2

In each of the question, show that the given differential equation is homogeneous and solve each of them.

3

In each of the question, show that the given differential equation is homogeneous and solve each of them.
(x – y)dy – (x + y)dx = 0

4

In each of the question, show that the given differential equation is homogeneous and solve each of them.
(x² – y²)dx + 2xy dy = 0

5

In each of the question, show that the given differential equation is homogeneous and solve each of them.

6

In each of the question, show that the given differential equation is homogeneous and solve each of them.

7

In each of the question, show that the given differential equation is homogeneous and solve each of them.

8

In each of the question, show that the given differential equation is homogeneous and solve each of them.

9

In each of the question, show that the given differential equation is homogeneous and solve each of them.

10

In each of the question, show that the given differential equation is homogeneous and solve each of them.

11

For each of the differential equations in question, find the particular solution satisfying the given condition:
(x + y)dy + (x – y) dx = 0; y = 1 when x = 1

12

For each of the differential equations in question, find the particular solution satisfying the given condition:
x²dy + (xy + y²)dx = 0; y = 1 when x = 1

13

For each of the differential equations in question, find the particular solution satisfying the given condition:

14

For each of the differential equations in question, find the particular solution satisfying the given condition:
y = 0 when x = 1

15

For each of the differential equations in question, find the particular solution satisfying the given condition:

16

A homogeneous differential equation of the from can be solved by making the substitution.

17

A homogeneous differential equation of the from can be solved by making the substitution.