Prove that x 2 – y 2 = c (x 2 + y 2 ) 2 is the general solution of differential equation (x 3 –3xy 2 ) dx = (y 3 –3x 2 y)dy, where c is a parameter.

Question

Philoid · Accepted Answer

It is given that (x³–3xy²) dx = (y³–3x²y)dy

- --------(1)

Now, let us take y = vx

Now, substituting the values of y and in equation (1), we get,

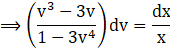
On integrating both sides we get,

--------(2)

Now,

---------(3)

Let

⇒

Now,

Let v² = p

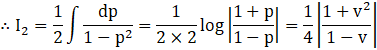
Now, substituting the values of I₁ and I₂ in equation (3), we get,

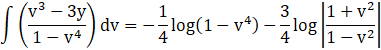
Thus, equation (2), becomes,

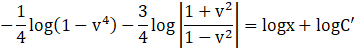
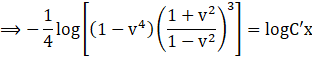
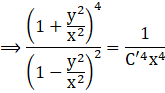
⇒ (x² – y²)² = C’⁴(x² + y² )⁴

⇒ (x² – y²) = C’²(x² + y² )

⇒ (x² – y²) = C(x² + y² ), where C = C’²

Therefore, the result is proved.