A bag contains 4 red and 4 black balls, another bag contains 2 red and 6 black balls. One of the two bags is selected at random and a ball is drawn from the bag which is found to be red. Find the probability that the ball is drawn from the first bag.
Given: let E1 be the event of choosing the bag I, E2 be the event of choosing the another bag say bag II and A be the event of drawing a red ball.
Then P (E1) = P (E2) = 1/2
Also P(A|E1) = P (drawing a red ball from bag I) ![]()
And P(A|E2) = P (drawing a red ball from bag II) ![]()
Now the probability of drawing a ball from bag I, being given that it is red, is P(E1|A).
By using bayes’ theorem, we have:
![]()
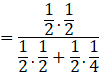
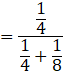
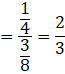
![]()
3