There are three coins. One is a two headed coin (having head on both faces), another is a biased coin that comes up heads 75% of the time and third is an unbiased coin. One of the three coins is chosen at random and tossed, it shows heads, what is the probability that it was the two headed coin?
Given: let E1 be the event of choosing a two headed coin, E2 be the event of choosing a biased coin and E3 be the event of choosing an unbiased coin. Let A be the event that the coin shows head.
Then P (E1) = P (E2) = P (E3) = 1/3
As we a headed coin has head on both sides so it will shows head.
Also P(A|E1) = P (correct answer given that he knows) = 1
And P(A|E2) = P (coin shows head given that the coin is biased) ![]()
And P(A|E3) = P (coin shows head given that the coin is unbiased) ![]()
Now the probability that the coin is two headed, being given that it shows head, is P(E1|A).
By using bayes’ theorem, we have:
![]()
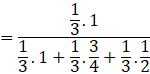
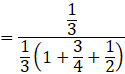
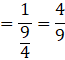
![]()