Suppose a girl throws a die. If she gets a 5 or 6, she tosses a coin three times and notes the number of heads. If she gets 1, 2, 3 or 4, she tosses a coin once and notes whether a head or tail is obtained. If she obtained exactly one head, what is the probability that she threw 1, 2, 3 or 4 with the die?
Given: : let E1 be the event that the outcome on the die is 5 or 6, E2 be the event that the outcome on the die is 1, 2, 3 or 4 and A be the event getting exactly head.
Then ![]()
And ![]()
As in throwing a coin three times we get 8 possibilities.
{HHH, HHT, HTH, THH, TTH, THT, HTT, TTT}
⇒ P(A|E1) = P (obtaining exactly one head by tossing the coin three times if she get 5 or 6) ![]()
And P(A|E2) = P (obtaining exactly one head by tossing the coin three times if she get 1,2 ,3 or 4) ![]()
Now the probability that the girl threw 1, 2, 3 or 4 with a die, being given that she obtained exactly one head, is P(E2|A).
By using bayes’ theorem, we have:
![]()
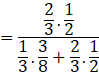
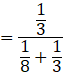
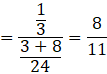
![]()