A card from a pack of 52 cards is lost. From the remaining cards of the pack, two cards are drawn and are found to be both diamonds. Find the probability of the lost card being a diamond.
Given: let E1 be the event that the drawn card is a diamond, E2 be the event that the drawn card is not a diamond and A be the event that the card is lost.
As we know, out of 52 cards, 13 cards are diamond and 39 cards are not diamond.
Then ![]()
And ![]()
Now, when a diamond card is lost then there are 12 diamond cards out of total 51 cards.
Two diamond cards can be drawn out of 12 diamond cards in 12C2 ways.
Similarly, Two diamond cards can be drawn out of total 51 cards in 51C2 ways.
Then probability of getting two cards, when one diamond card is lost, is P(A|E1).
Also P(A|E1) =12C2 / 51C2
![]()
![]()
![]()
Now, when not a diamond card is lost then there are 13 diamond cards out of total 51 cards.
Two diamond cards can be drawn out of 13 diamond cards in 13C2 ways.
Similarly, Two diamond cards can be drawn out of total 51 cards in 51C2 ways.
Then probability of getting two cards, when card is lost which is not diamond, is P(A|E2).
Also P(A|E2) =13C2 / 51C2
![]()
![]()
![]()
Now the probability that the lost card is diamond, being given that the card is lost, is P(E1|A).
By using Bayes’ theorem, we have:
![]()
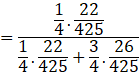
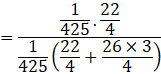
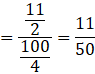
![]()