A random variable X has the following probability distribution:
X | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
P(X) | 0 | k | 2k | 2k | 3k | K2 | 2 K2 | 7 K2 + k |
Determine
(i) k (ii) P(X < 3)
(iii) P(X > 6) (iv) P(0 < X < 3)
Given: A random variable X with its probability distribution.
(i) As we know the sum of all the probabilities in a probability distribution of a random variable must be one.
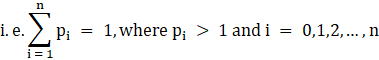
Hence the sum of probabilities of given table:
⇒ 0 + k + 2k + 2k + 3k + k2 + 2k2 + 7K2 + k = 1
⇒ 10K2 + 9k = 1
⇒ 10K2 + 9k – 1 = 0
⇒ (10K-1)(k + 1) = 0
![]()
It is known that probability of any observation must always be positive that it can’t be negative.
So ![]()
(ii) P(X < 3) = ?
P(X < 3) = P(X = 0) + P(X = 1) + P(X = 2)
= 0 + k + 2k
= 3k
![]()
(iii) P(X > 6) = ?
P(X > 6) = P(X = 7)
= 7K2 + k
![]()
![]()
![]()
(iv) P(0 < X < 3) = ?
P(0 < X < 3) = P(X = 1) + P(X = 2)
= k + 2k
= 3k
![]()