The random variable X has a probability distribution P(X) of the following form, where k is some number:
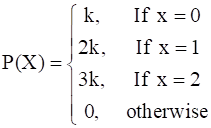
(a) Determine the value of k.
(b) Find P (X < 2), P (X ≤ 2), P(X ≥ 2).
Given: A random variable X with its probability distribution.
(a) As we know the sum of all the probabilities in a probability distribution of a random variable must be one.

Hence the sum of probabilities of given table:
⇒ k + 2k + 3k + 0 = 1
⇒ 6k = 1
![]()
(b) (i) P(X < 2) = ?
P(X < 2) = P(X = 0) + P(X = 1)
= k + 2k
= 3k
![]()
(ii) P(X ≤ 2) = ?
P(X ≤ 2) = P(X = 0) + P(X = 1) + P(X = 2)
= k + 2k + 3k
= 6k
![]()
(iii) P(X ≥ 2) = ?
P(X ≥ 2) = P(X = 2) + P(X > 2)
= 3k + 0
= 3k
![]()
9