Find the mean number of heads in three tosses of a fair coin.
Given: A coin is tossed three times.
three coins are tossed simultaneously. Hence, the sample space of the experiment is S = {HHH, HHT, HTH, THH, TTH, THT, HTT, TTT}
X represents the number of heads.
As we see, X is a function on sample space whose range is {0, 1, 2, 3}.
Thus, X is a random variable which can take the values 0, 1, 2 or 3.
P(X = 0) = P(TTT) ![]()
P(X = 1) = P(TTH) + P(THT) + P(HTT) ![]()
P(X = 2) = P(THH) + P(HTH) + P(HHT) ![]()
P(X = 3) = P(HHH) ![]()
Hence, the required probability distribution is,
X | 0 | 1 | 2 | 3 |
P(X) |
|
|
|
|
Therefore mean μ is:
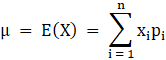
![]()
![]()
![]()
10