Given: Two fair dice are rolled

When two fair dice are rolled then number of observations will be 6 × 6 = 36.

X denote the sum of the numbers obtained when two fair dice are rolled. Hence, X can take any value of 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 or 12.

For X = 2, the possible observations are (1, 1).

For X = 3, the possible observations are (1,2) and (2,1)

For X = 4, the possible observations are (1,3), (2,2) and (3,1).

For X = 5, the possible observations are (1, 4), (4, 1), (2,3) and (3,2)

For X = 6, the possible observations are (1, 5), (5, 1), (2,4), (4,2) and (3,3).

For X = 7, the possible observations are (1, 6), (6, 1), (2,5), (5,2),(3,4) and (4,3).

For X = 8, the possible observations are (2,6), (6,2),(3,5), (5,3) and (4,4).

For X = 9, the possible observations are (5, 4), (4, 5), (3,6) and (6,3)

For X = 10, the possible observations are (5,5), (4,6) and (6,4).

For X = 11, the possible observations are (6,5) and (5,6)

For X = 12, the possible observations are (6, 6).

Hence, the required probability distribution is,

Therefore E(X) is:

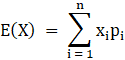
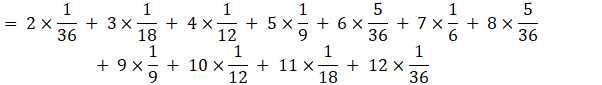
⇒ E(X) = 7

And E(X²) is:

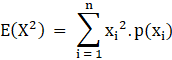
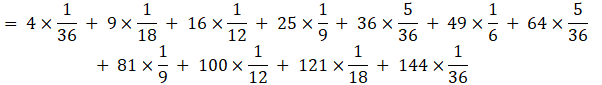
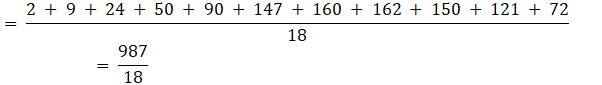
⇒ E(X²) = 54.833

Then Variance, Var(X) = E(X²) – (E(X))²

= 54.833 – (7)²

= 54.833 – 49 = 5.833

And Standard deviation

⇒ Standard deviation = 2.415